07. Matrix Multiplication - General
So far we only concentrated on square matrix multiplications. However, we are not limited to square matrices alone.
Lets look again at our image that represents the multiplication P x Q :
Remember, the order here does matter, as matrix multiplication is not commutative
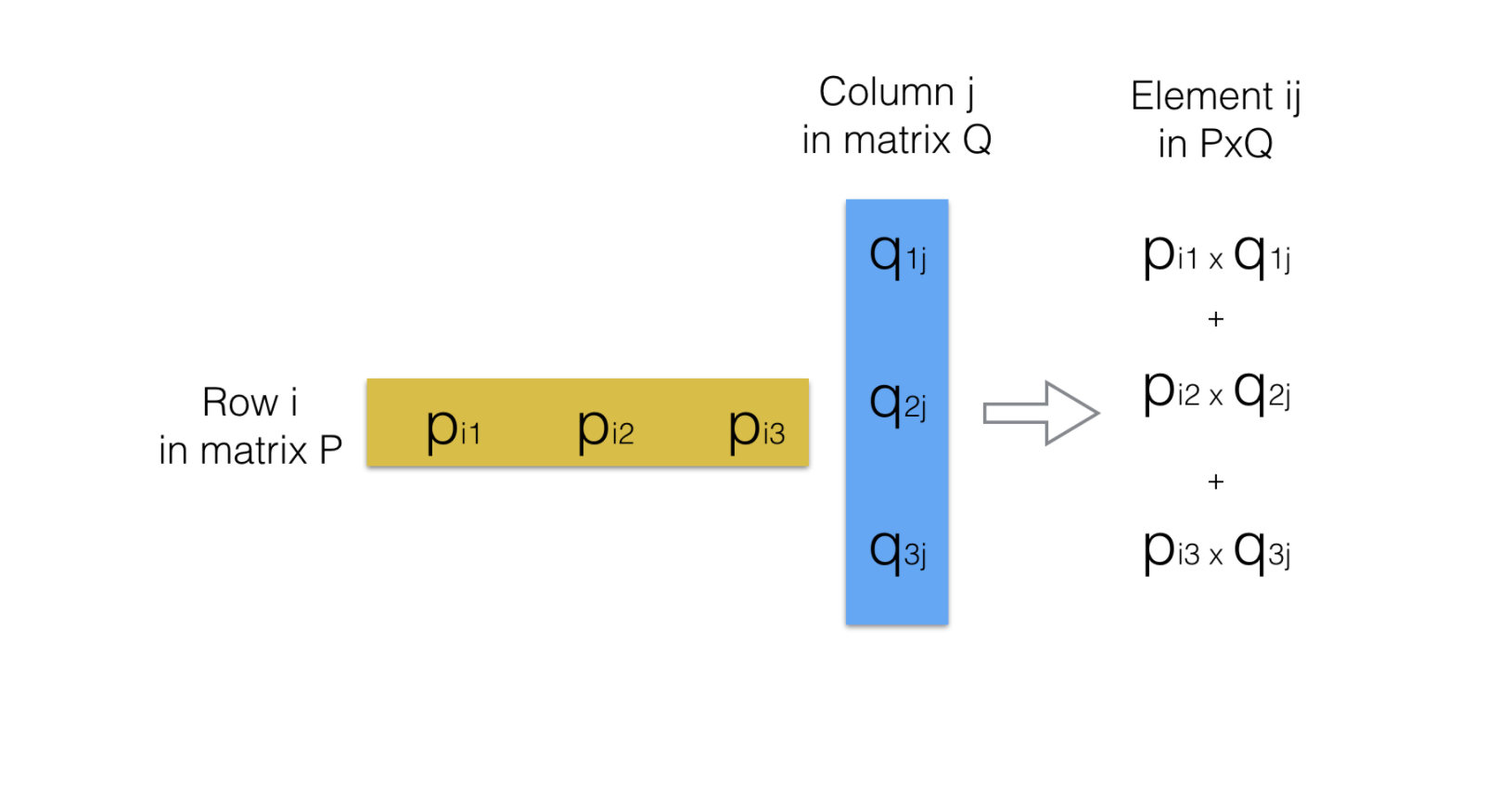
If you look closely at the image that represents the multiplication of P x Q , you will see that the number columns in P equals the number of rows in Q . (In the case of our example, it was 3 ).
How many rows do we have in matrix P ? How many columns do we have in matrix Q ? That will deretmine the dimensions of the resulting multiplication.
In other words, if P is a matrix with dimensions t x m and Q is a matrix with dimensions m x v then:
-
P x Q is possible as the dimensions match. ( P has m columns and Q has m rows).
-
P x Q will be a matrix of t x v . ( t rows and v columns).
Lets look at an example:
P=\begin{bmatrix} p_{11} &p_{12} &p_{13}\\ p_{21} &p_{22} &p_{23}\end{bmatrix}
Q=\begin{bmatrix} q_{11} &q_{12}&q_{13}&q_{14}\\ q_{21} &q_{22}&q_{23}&q_{24} \\q_{31} &q_{32}&q_{33}&q_{34}\end{bmatrix}
We would like to calculate P x Q .
Our first step is to see if the calculation is possible. We will do that by looking at the dimensions of the matrices.
Matrix P has 3 columns and matrix Q has 3 rows. Perfect! multiplication is possible.
We expect to have a final result P x Q with the dimensions 2 x 4 ( 2 rows and 4 columns).
P x Q = \begin{bmatrix} p_{11}q_{11}+p_{12}q_{21}+p_{13}q_{31} &p_{11}q_{12}+p_{12}q_{22}+p_{13}q_{32} &p_{11}q_{13}+p_{12}q_{23}+p_{13}q_{33} &p_{11}q_{14}+p_{12}q_{24}+p_{13}q_{34}\\ p_{21}q_{11}+p_{22}q_{21}+p_{23}q_{31} &p_{21}q_{12}+p_{22}q_{22}+p_{23}q_{32} &p_{21}q_{13}+p_{22}q_{23}+p_{23}q_{33}&p_{21}q_{14}+p_{22}q_{24}+p_{23}q_{34}\end{bmatrix}
Equation 16